Programme de seconde générale et technologique 2019
« Représenter un nuage de points associé à la caractéristique d’un dipôle et modéliser la caractéristique de ce dipôle à l’aide d’un langage de programmation. »
Exemple : caractéristique d’une CTN
Cas d’un capteur de température NTC 10K type EKS 221.
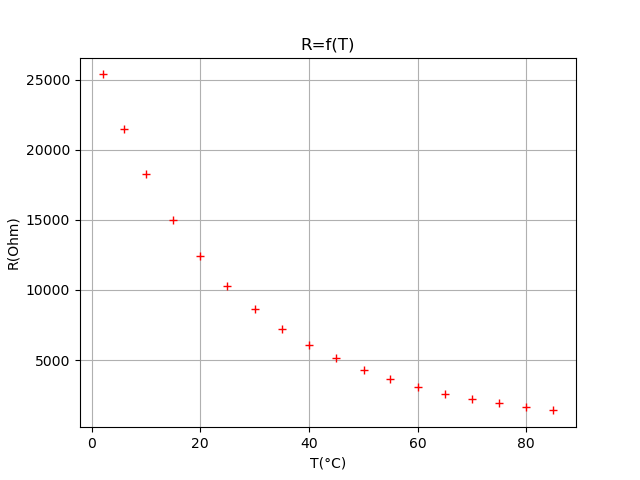
Programme simple
import numpy as np
import matplotlib.pyplot as plt
T = np.array([2, 6, 10, 15, 20, 25, 30, 35, 40, 45, 50.1, 55, 60, 65, 70, 75, 80, 85])
R = np.array([25378,21487,18301,14990,12402,10295,8615,7226,6097,5121,4306,3632,3070,2609,2221,1903,1630,1404])
plt.plot(T,R,'r+') # Tracé du nuage de points en rouge
plt.title('R=f(T)') # Ajout d'un titre
plt.xlabel('T(°C)') # Ajout d'une légende sur l'abscisse
plt.ylabel('R(Ohm)') # Ajout d'une légende sur l'ordonnée
plt.grid() # Ajoute une grille
plt.show() # Affiche la figure
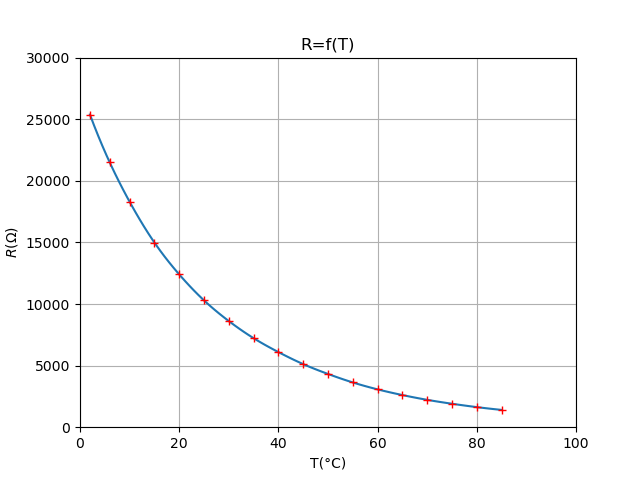
Programme évolué
Avec en plus une interpolation, une échelle manuelle, un texte mathématique en LaTex, …
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
T = np.array([2, 6, 10, 15, 20, 25, 30, 35, 40, 45, 50.1, 55, 60, 65, 70, 75, 80, 85])
R = np.array([25378,21487,18301,14990,12402,10295,8615,7226,6097,5121,4306,3632,3070,2609,2221,1903,1630,1404])
#Interplotation
f = interpolate.interp1d(T, R, kind='cubic') # Interpolation à partir des mesures
Tint = np.linspace(T.max(),T.min(),100) # Calcul de l'abscisse
Rint = f(Tint) # Calcul de la résistance
plt.plot(Tint,Rint) # Tracé de l'interpolation
plt.plot(T,R,'r+') # Tracé du nuage de points en rouge
plt.title('R=f(T)') # Ajout d'un titre
plt.xlabel('T(°C)') # Ajout d'une légende sur l'abscisse
plt.xlim(0,100) # Fixe l'échelle sur l'abscisse
plt.ylabel('$R(\Omega)$') # Ajout d'une légende sur l'ordonnée en LaTex
plt.ylim(0,30000) # Fixe l'échelle sur l'abscisse
plt.grid() # Ajoute une grille
plt.show() # Affiche la figure